Solutions to HW #1: *.ps *.pdf
-
p. 667: 18.1, 18.2, 18.3, 18.4, 18.5, 18.16, 18.17
Solutions to HW #2: *.ps *.pdf
Non-Riley problems:
- Evaluate the integrals of exp(1/z), sin(1/z) and cos(1/z) around the contour |z|=1.
- Evaluate the integral
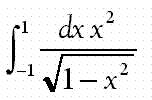 using contour integration on an appropriately
chosen contour.
using contour integration on an appropriately
chosen contour.
- Evaluate the integral
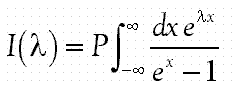 and show that it is equal to
and show that it is equal to 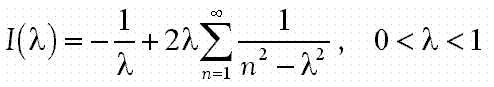 . Thence evaluate the sums of n–2 and n–4 from n=1 to infinity. The P means “take the Cauchy principal value”.
. Thence evaluate the sums of n–2 and n–4 from n=1 to infinity. The P means “take the Cauchy principal value”.
Due: 10/17/2000, 17:00 my office (Rm 312D)
Solutions to HW #3: *.ps *.pdf
Non-Riley problem:
Read the material dealing with the driven damped harmonic oscillator in the linked chapter from my notes on classical mechanics. Confirm that the Langevin equation has the solution for x(t) given on p. 65. Confirm that the formula for the velocity is as given on p. 66. If the driving force is random, with statistical properties
 ,
, 
verify the formulas for variance of position and velocity on p.68 . Then verify the formulas on p. 69. (There may be typos; also, the definition I gave for the damping in class differs from that in these CM notes by a factor m.) Finally, verify that the limit for w—>0 is as given on p. 69.
Due: 11/15/2001, 17:00 my office (Rm 312D)
Solutions to HW #4 (in *.pdf format)
 Read Riley, Chapters 15–17; 20–21 and my notes also.
Read Riley, Chapters 15–17; 20–21 and my notes also.
HW: Riley, et al.
Non-Riley problems:
- What is the differential equation satisfied by the function
y(x) = xa J±m(bxg ) ?
Use this result to find the eigenvalues of the swinging chain. (This is a uniform suspended chain whose lower end is free—thus the restoring force is gravitational. The displacement of a point along the chain obeys a linear, second-order pde that we discussed in class:
where x=0 is the lower—free—end of the chain and x=L is the upper end.)
- Energy in a star is produced in nuclear reactions initiated by collisions. If the number of collisions per unit time, of particles with CM kinetic energy between E and E+dE is NEe–E/Q, where N is a constant and Q=kBT is the absolute temperature in energy units; and if the probability that a collision will result in a reaction is Me–a/ÖE (again M and a are constants) use the method of steepest descents to estimate the rate of nuclear reactions assuming (Q/a²)1/6«1.
- Apply the Gram-Schmidt orthogonalization method to the monomials x0, x1, and x2 to derive the first 3 Hermite polynomials H0, H1, and H2, where these polynomials are orthogonal on the interval (–¥, +¥) with respect to the weight function e–x². Do not bother to normalize the polynomials.
- The Schrödinger equation of the hydrogenic atom is

Estimate the ground state energy using the trial function e–lr².
- Solve the integral equation

- Consider the operator defined by the kernel

- Show that it is Hermitian.
- Show that its eigenvalue spectrum is countably infinite.
- Show that it represents a positive-definite operator.
- Show it is bounded.
- Show that it is compact.
- Evaluate the integral

for arbitrary values of the dimensionality d. Hint: evaluate the angular factor, W(d), using the identity
and using the definition of the G function.
What is the nature of the singularity as d goes to 4? (The parameter L is a “running scale” with dimensionality the same as D.)
You will need to use the properties of the G function for this.
Solutions to HW #5 in *.ps format (*.pdf)
Due: December 6, 2000, 16:00 my office (Rm 312D)
